“Minions: The Rise of Gru” was pretty good, and tells the origin story of Gru and his formative years. That’s all well and good, but the waterfall trap scene was the most interesting piece of the movie to me. The movie opens with some villains attempting to steal this mystical artifact from a temple. In order to get into the temple the villain must reorient these dragons which blow fire to clear away the falling water by turning it to steam. Is this even possible, and if so how much heat would it take, and why wouldn’t the opener be singed by the overwhelming temperatures?
The Trap/Lock Setup
The villain encounters a waterfall with 2 dragon statues, by turning 2 smaller dragons he causes the larger statues to turn and emit flame. These flames provide enough heat to reveal a door behind the waterfall by turning the falling water to steam. It sort of looked like this ms paint diagram.

The Problem Setup
Given a waterfall of width \(w\), depth \(d\), and height \(h\) calculate how much water is flowing. Use the volume calculated to determine how much water mass is actually flowing. Then use the specific heat formulas to determine how much energy needs to be added to convert the water to steam. Finally, we calculate how much natural gas would be used in this operation.
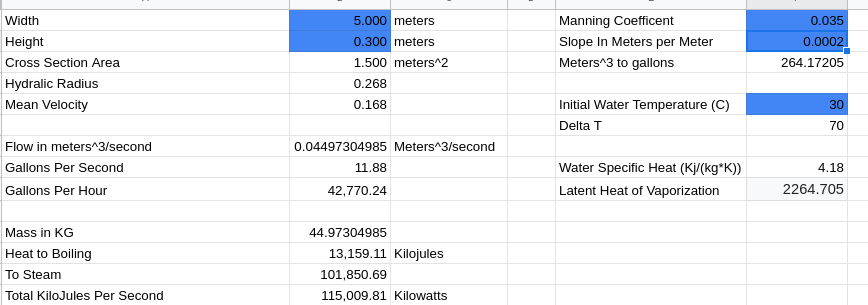
The discharge \(Q\) in cubic meters is calculated by determining the mean flow velocity, and then using the cross sectional area. The formulas can be found in this PDF.
\[V=\frac{1}{n}R^{2/3}\sqrt{S}\] \[Q= aV = \frac{1}{n}aR^{2/3}\sqrt{S}\]Some of the values are weird, but just go with it. \(n\) is the Manning coefficient of roughness, which computes the friction in a water channel as I understand it. \(R\) is the wetted perimeter which is also known as the hydraulic radius. \(S\) is the slope in meters over meters, or how steep the gradient of the river is.
From here the next step is to convert the cubic meters of water into kilograms because that’s what thermodynamic equations use. That’s an easy calculation since water is roughly a 1000kg per meter cubed.
Next using the specific heat equation, the amount of energy required to heat the water to the boiling point can be computed. Then we can use the latent heat of vaporization \(L\) to compute the amount of heat needed to be steam. The latent heat is how much energy is buffered before things change state.
\[Q_{heat} = m\Delta{T}c + mL\]\(c\) is the specific heat in joules per kilogram. \(\Delta{T}\) is the total change in temperature. To determine \(\Delta{T}\), a starting temperature and something like 30 degrees Celsius sounds right, water boils a 100 degrees, that makes the \(\Delta{T}=70\). \(L\) is the latent heat, as always \(m\) is the mass.
After all of these equations we have the power required to vaporize the water falling each second, but we need to know if it’s even possible. So let’s plug some toy numbers into these equations using excel. A 5 meter wide waterfall with about a foot of depth would deliver 11 gallons of water per second, assuming 1 meter drop per 5 kilometers. This would require 115,000 kilowatts to vaporize to steam. This would be equivalent to 1/10th the power of the space shuttle at launch according to wolfram alpha.
As it could probably be assumed, making a waterfall door that cool would be clearly impossible for just about any civilization. Especially, since it’s not like that much water would crush you. You could easily just walk right on through it. As such this door would be a really stupid solution, and well beyond the capabilities of most civilizations. (I would assume anyone who tried to use it would be burned alive).